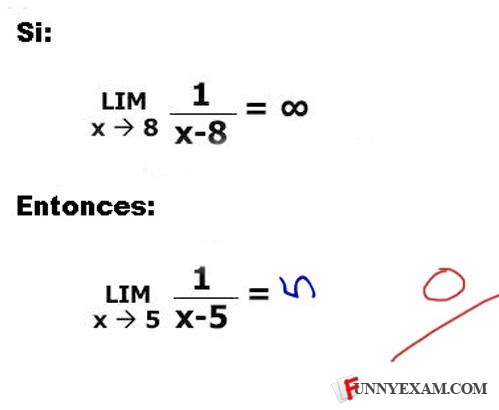
Other's Responses
-
Cheaters never prosper. 13KeyClick + Refresh = You now have a very very negative score, sir.
-
This made me laugh, I'll admit.
-
In logics, student wins.
-
lawls..... SIMPLICITY FTW
-
public school has no appreciation for right brainers
-
If we apply your way of thinking, you actually got a "10" instead of a "0".
-
i actually laughed my ass off on this one....who new calc was that easy?
-
Stupid questions get stupid answers.
-
As you can see up the top..... YOLO :D
-
si= if entonces=then
-
hahahahabahhaahahahahahahahahaha that was so hilarious!!!!!! XDDDDDD
-
This was brilliant
-
Mark = Infinite 10s
-
lim i/(X-8) when x->8 is an indertermination...
-
that was so easy... infinite.. but the boy or girl was pretty smart hehe
-
From the right and left lim of 1/0 does not exist. Firstly one nulth does not exist... Right side equal + infinity, and left side - infinity, left and right sided limits differs, so lim(x->8) for 1/(x-8), does not have lim in 8, as well as lim(x->5) for 1/(x-5). But I agree, perfect answer for incorrect question.
-
but... the limit as x approaches 8 of 1/(x-8) is undefined!
-
if the mark is written the same way as the 5 and the 8, he's got 10 points ! lol
-
The example they provided would have been right had they specified that to find the right hand limit but since the limit of the right is infinity and the limit on the left is negative infinity the real answer would be undefined.
-
niu B
-
that's got to be the best one i seen yet :)
-
Retards don't know limits, the limit does not exist, so this is a teacher fail + fake
-
So we're assuming that's a right-hand limit, are we?
-
i know why... because he read the example by otherside of paper....hahaaha
-
I actually didn't see it at first, but this one's genius xD
-
should it have been in black ink? is that why its wrong?
-
The first limit actually doesn't exist :P
-
it says: "if the limit as x approaches 8 of 1 / (X - 8) approaches infinity, then what does the limit as x approaches 5 of 1 / (X - 5) approach?" Si = If Entonces = Then
-
THATS FXING SMART!
-
Genius
-
This is by far the funniest I've ever seen, lol.
-
8-8 is the same as 5-5 the answer is the fucking same, infinity
-
So, the student got a 10. Grats!
-
Classical! Oh, if Mr G. found this out he'll say: see me so we can discuss your method. 0. XDD
-
The 0 the teacher gave is probably sideways as well.
-
Oh so the answer isn't a sideways number?
-
Maybe the '5' was rotated the wrong way.
-
I don't get it. Oh yeah, I don't speak geek.
-
Ironically the example one is also wrong because both limits don't exist because as both of them approach their respective numbers from lower numbers, the limit approches negative infinity. However, the limit approches positive infinity when both numbers approach their respective numbers from higher numbers. Since overall limits only exist if they're the same on both sides, the ansver to both are undefined.
-
This is wrong. Should be negative infinity. Is funny, but yould be better if the math in the first example was done right.
-
I see nothing wrong good job!
-
-
I love it! I actually lmfao (:
-
luv it! lmao
-
oh christ on a cross wot a load of nobs do be commenting on this site. humourless nerds. oh, and the post is fkn funny, made me laff
-
depending on the funcion the top one is correct, the domain must not be 5 but when dealing witth irrational functions which mean's it's either a hole or non existand, but i phail to understand why you'd want to correct it because what matters is the 5 xDDDDDDD
-
8 is basically a sideways infinity. So x-infinity, is indeed infinity. Silly teachers.
-
This test is dumb. The limit of those functions do not exist. The limit from the left is negative infinity, and from the right it is positive infinity. The student is no more wrong than the teacher.
-
there to many number to get a chance to get this right
-
took me a while but... PERFECT answer:D
-
lmfaoo ahahha
-
I'll admit it took me a while. But I laughed.
-
mathematical reasoning.. we actually learn dat in skool..;p
-
umm i didnt get it :(
-
abstract reasoning ?? HAHHAHA !! ur on the wrong exam :P L.O.L :D
-
m
-
To you stupid pisscunts saying that the limit doesn't exist, LOOK AT THE FIRST WORD ON THE PAGE. It says "IF" the limit = infinity, meaning you apply the limit approaching from the right, not the left.
-
It wouldve been right if he turned the 5 around the other way.
-
I dont get it
-
the answer is 3
-
The limit actually does not exist, unless it's as X approaches 8 from either the positive side (in which case it's infinity) or the negative side (in which case it's negative infinity). Can't blame the kid for getting a wrong answer on a question with a false premise.
-
IT IS SO CLEAR NAO O_O
-
Lol ITs in Spanish.
-
Maybe it was supposed to be reasoning, not maths?!?!?
-
5 = True :3 Blv or Not
-
YOU...SHALL NOT....PAAAASSSSSSSSSSS!!!!!!
-
This is fake, my teacher showed it to my class as a joke line 5 years ago
-
Actually, the first limit doesn't tend to +inf. The left limit tends to -inf and the right limit tends to +inf, so the limit is not defined. But this is funny anyways.
-
public school has no appreciation for right brainers
-
WIN!
-
Made me laugh as do silly
-
Great twisting!
Cheaters never prosper. 13KeyClick + Refresh = You now have a very very negative score, sir.