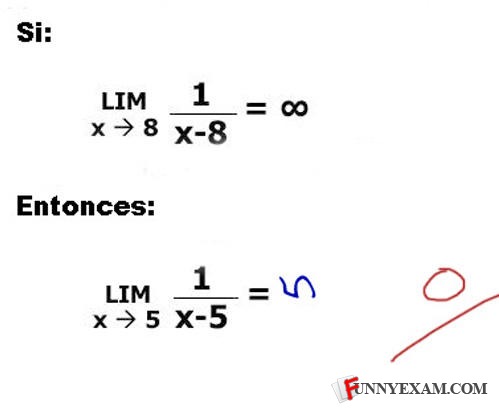
Other's Responses
-
Cheaters never prosper. 13KeyClick + Refresh = You now have a very very negative score, sir.
-
This made me laugh, I'll admit.
-
In logics, student wins.
-
lawls..... SIMPLICITY FTW
-
public school has no appreciation for right brainers
-
If we apply your way of thinking, you actually got a "10" instead of a "0".
-
i actually laughed my ass off on this one....who new calc was that easy?
-
Stupid questions get stupid answers.
-
si= if entonces=then
-
hahahahabahhaahahahahahahahahaha that was so hilarious!!!!!! XDDDDDD
-
Mark = Infinite 10s
-
As you can see up the top..... YOLO :D
-
lim i/(X-8) when x->8 is an indertermination...
-
that was so easy... infinite.. but the boy or girl was pretty smart hehe
-
This was brilliant
-
From the right and left lim of 1/0 does not exist. Firstly one nulth does not exist... Right side equal + infinity, and left side - infinity, left and right sided limits differs, so lim(x->8) for 1/(x-8), does not have lim in 8, as well as lim(x->5) for 1/(x-5). But I agree, perfect answer for incorrect question.
-
The example they provided would have been right had they specified that to find the right hand limit but since the limit of the right is infinity and the limit on the left is negative infinity the real answer would be undefined.
-
if the mark is written the same way as the 5 and the 8, he's got 10 points ! lol
-
but... the limit as x approaches 8 of 1/(x-8) is undefined!
-
niu B
-
Retards don't know limits, the limit does not exist, so this is a teacher fail + fake
-
So we're assuming that's a right-hand limit, are we?
-
I actually didn't see it at first, but this one's genius xD
-
should it have been in black ink? is that why its wrong?
-
i know why... because he read the example by otherside of paper....hahaaha
-
that's got to be the best one i seen yet :)
-
THATS FXING SMART!
-
The 0 the teacher gave is probably sideways as well.
-
8-8 is the same as 5-5 the answer is the fucking same, infinity
-
The first limit actually doesn't exist :P
-
Oh so the answer isn't a sideways number?
-
This is by far the funniest I've ever seen, lol.
-
I see nothing wrong good job!
-
Maybe the '5' was rotated the wrong way.
-
Classical! Oh, if Mr G. found this out he'll say: see me so we can discuss your method. 0. XDD
-
it says: "if the limit as x approaches 8 of 1 / (X - 8) approaches infinity, then what does the limit as x approaches 5 of 1 / (X - 5) approach?" Si = If Entonces = Then
-
So, the student got a 10. Grats!
-
Genius
-
I love it! I actually lmfao (:
-
I don't get it. Oh yeah, I don't speak geek.
-
luv it! lmao
-
This test is dumb. The limit of those functions do not exist. The limit from the left is negative infinity, and from the right it is positive infinity. The student is no more wrong than the teacher.
-
This is wrong. Should be negative infinity. Is funny, but yould be better if the math in the first example was done right.
-
Ironically the example one is also wrong because both limits don't exist because as both of them approach their respective numbers from lower numbers, the limit approches negative infinity. However, the limit approches positive infinity when both numbers approach their respective numbers from higher numbers. Since overall limits only exist if they're the same on both sides, the ansver to both are undefined.
-
oh christ on a cross wot a load of nobs do be commenting on this site. humourless nerds. oh, and the post is fkn funny, made me laff
-
8 is basically a sideways infinity. So x-infinity, is indeed infinity. Silly teachers.
-
-
depending on the funcion the top one is correct, the domain must not be 5 but when dealing witth irrational functions which mean's it's either a hole or non existand, but i phail to understand why you'd want to correct it because what matters is the 5 xDDDDDDD
-
there to many number to get a chance to get this right
-
m
-
lmfaoo ahahha
-
mathematical reasoning.. we actually learn dat in skool..;p
-
It wouldve been right if he turned the 5 around the other way.
-
took me a while but... PERFECT answer:D
-
I dont get it
-
the answer is 3
-
To you stupid pisscunts saying that the limit doesn't exist, LOOK AT THE FIRST WORD ON THE PAGE. It says "IF" the limit = infinity, meaning you apply the limit approaching from the right, not the left.
-
Maybe it was supposed to be reasoning, not maths?!?!?
-
abstract reasoning ?? HAHHAHA !! ur on the wrong exam :P L.O.L :D
-
Lol ITs in Spanish.
-
The limit actually does not exist, unless it's as X approaches 8 from either the positive side (in which case it's infinity) or the negative side (in which case it's negative infinity). Can't blame the kid for getting a wrong answer on a question with a false premise.
-
5 = True :3 Blv or Not
-
umm i didnt get it :(
-
I'll admit it took me a while. But I laughed.
-
This is fake, my teacher showed it to my class as a joke line 5 years ago
-
YOU...SHALL NOT....PAAAASSSSSSSSSSS!!!!!!
-
IT IS SO CLEAR NAO O_O
-
Made me laugh as do silly
-
Actually, the first limit doesn't tend to +inf. The left limit tends to -inf and the right limit tends to +inf, so the limit is not defined. But this is funny anyways.
-
Great twisting!
-
WIN!
-
public school has no appreciation for right brainers
Cheaters never prosper. 13KeyClick + Refresh = You now have a very very negative score, sir.